|
Author: A. Betti
In this tutorial, we will write a python script to compute the electron and phonon dispersion curves of an armchair GNR, and then the momentum relaxation rates for absorption (ABS) and emission (EM) of both acoustic (AC) and optical (OP) phonons.
Let’s import the module as usual
from NanoTCAD_ViDES import *
Let’s define an armchair nanoribbon with 10 dimer lines, where dimer lines are defined as in Tutorial 02: nanoribbon:
a=GNRphonon(10)
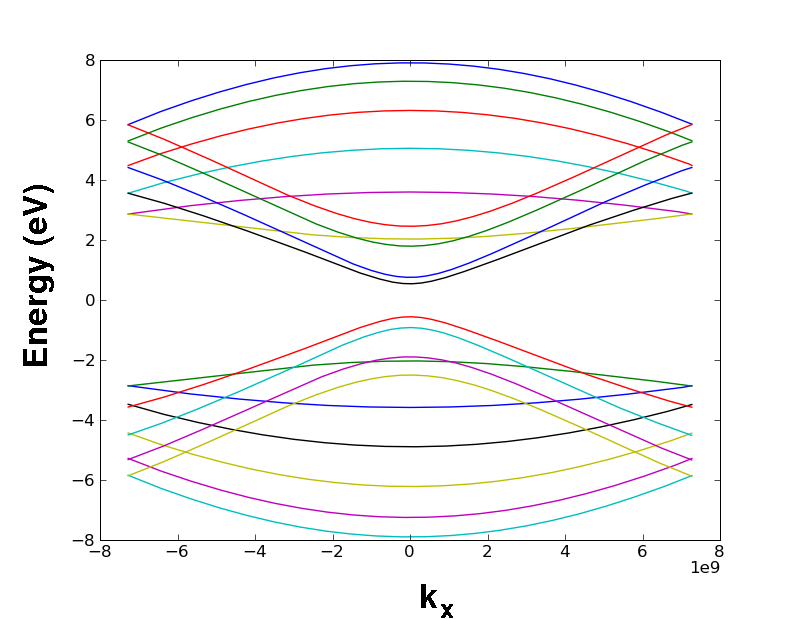
Then we compute the GNR electron subbands:
electron_GNR(a)
The informations of the electron spectra are now stored in the matrix energyE.
Note that in the code the longitudinal electron wavevector is kx and the longitudinal phonon wavevector is defined as qx, whereas, for what concerns the transverse wavevectors, we use kyE for electrons and qy for phonons. Instead the couple (qx0,qy0) indicates the specific point of the reciprocal space where the graphene branches are computed. Of course kx=qx: the discretization is the same. The quantities kx,qx,kyE,qy,qx0,qy0 are obviously attributes of the class a, as described in GNRphonon. In order to plot the whole energy spectra as a function of the longitudinal electron wavevector kx, we can write:
plot(a.kx,a.energyE[:,:])
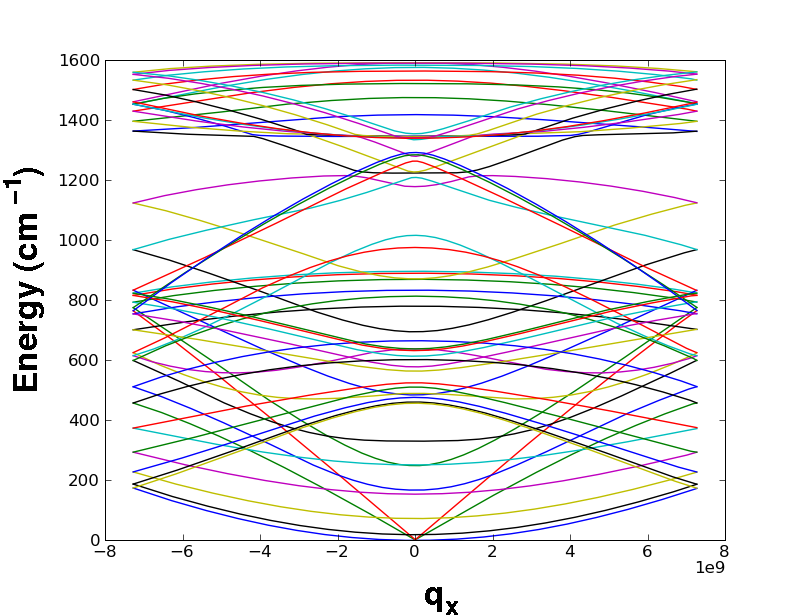
Then we calculate the GNR phonon spectra, as in the following:
phonon_GNR(a)
The phonon dispersion curves are stored in the matrix energyP2D. The full phonon spectra can then be plotted by writing:
plot(a.qx,a.energyP2D[:,:])
Once the electron and phonon dipersion curves are known, we can compute scattering rates. As explained in GNRphonon, it is possible to simulate both LA and TA modes within the Deformation potential approximation (DPA) by setting numberAC=2, wherenumberAC is an attribute of the class a. By imposing numberAC=1, only the effect of LA modes on electron transport is taken into account.
When computing rates, it is also possible to choose a sampling along the kx direction by setting the value of delta, an attribute of a.
The momentum relaxation rates corresponding to absorption and emission of acoustic phonons can be easily obtained as in the following:
rateACABS(a)
rateACEM(a)
By calling the function rateACABS (rateACEM), scattering rates for ABS (EM) of AC phonons are stored in the matrix rateAA (rateAE). If one wants to plot the scattering rate corresponding to the ABS process of AC phonons for an electron in the initial electron subband with index m, it is sufficient to write:
plot(a.energyE[:,m],a.rateAA[:,m])
It is important to understand that rates are only computed for energies smaller than a specified electron energy Ecutoff, which is an attribute of the class a (see GNRphonon). This involves that for electron subbands higher than Ecutoff the corresponding scattering rate rateAA is zero for all initial electron energies in the subband. Rates are different from zero for only the lowest electron subbands, having a quantum number m generally close to (# of dimer) / 2.
For example, for (# of dimer)=10, m=6 and m=7 correspond to the first and the second subbands, respectively. If delta>1, it can be convenient to plot rateAA by using points, rather than a line:
plot(a.energyE[:,m],a.rateAA[:,m],’o’)
In the same way, scattering rates involving absorption and emission of optical phonons can be calculated:
rateOPTABS(a)
rateOPTEM(a)
By calling the function rateOPTABS (rateOPTEM), scattering rates for ABS (EM) of OPT phonons are stored in the matrix rateOA (rateOE)
If one wants to plot the scattering rate corresponding to the EM process of OPT phonons for an electron in the initial electron subband with index m, it is sufficient to write:
plot(a.energyE[:,m],a.rateOE[:,m]) As already remarked above and discussed in the Commands/Class GNRphonon, qx0 and qy0 are attributes of a and can be defined in the file “NanoTCAD_ViDES.py”. For example, we can be interested to calculate the phonon branches in the point Gamma of the Brillouin zone, therefore we define qx0=0 and qy0=0. Then we have to compile the program and finally to run it by writing:
phonon_graphene(a)The graphene phonon energy are expressed in cm-1 (1cm-1 = 0.124 meV).
|