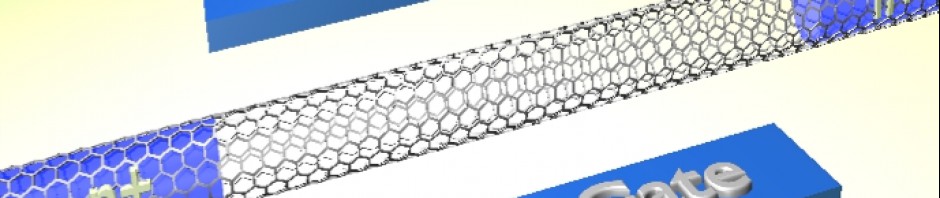
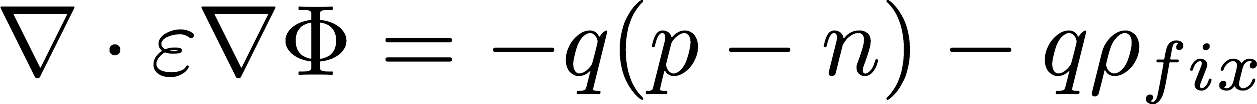Synopsys: solve_self_consistent(grid3D,interface3D,NEGF_class)
From a numerical point of view, the code is based on the Newton-Raphson (NR) method with a predictor/corrector scheme [A. Trellakis, A. T. Galick, A. Pacelli, and U. Ravaioli, “Iteration scheme for the solution of the two-dimensional Schrödinger–Poisson equations in quantum structures,” J. Appl. Phys, vol. 81, pp. 7800–7804, 1997.]. In the figure below, we sketch a flow-chart of solve_self_consistent.
In particular, the Schr ̈odinger/NEGF equations are solved at the beginning of each NR cycle, starting from an initial potential Φ ̃ (attribute Phiold of the classinterface3D), and the charge density in the NEGF_class is kept constant until the NR cycle converges (i.e. the correction on the potential is smaller than a predetermined value). The algorithm (solve_Poisson) is then repeated cyclically until the norm of the difference between the potential computed at the end of two subsequent NR cycles is smaller than a predetermined value (smaller than normd specified in interface3D class)
Some convergence problems however may be encountered using this iterative scheme. Indeed, since the electron density is independent of the potential within a NR cycle, the Jacobian is null for points of the domain including the NEGF_class region, losing control over the correction of the potential. We have used a suitable expression for the charge predictor, in order to give an approximate expression for the Jacobian at each step of the NR cycle. To this purpose, we have used an exponential function for the predictor In particular, if C is the free charge (free_charge in interface3D), the charge density Ci at the i-th step of the NR cycle can be expressed as
where φ ̃ and φi (attribute Phi of the class interface3D) are the electrostatic potentials computed at the first and i-th step of the NR cycle, respectively, and VT is the thermal voltage. Since the charge density C is extremely sensitive to small changes of the electrostatic potential between two NR cycles, the exponential function acts in the overall procedure as a dumping factor for charge variations. In this way, convergence has been improved in the subthreshold regime and in the strong inversion regime. Convergence is still difficult in regions of the device where the charge is not compensated by fixed charge, where the right-hand term of the Poisson equation is considerably large.
Related tutorial: Tutorial 05