Synopsys: bilayer_graphene(L)
bilayer_graphene is the NanoTCAD ViDES class for bilayer graphene flake. As inputs, it requires the length of the bilayer graphene flake L expressed in nanometers.
The structure is similar to the one explained in the graphene class, where the simulation domain is long L nanometer (in the case shown above, 2 elementary cell constituted by 16 atoms, 8 at the bottom (circles) and 8 at the top (crosses)).
The bilayer graphene flake is then repeated along the y direction attaching semi-infinite leads through the definition of the self-energy ∑, while in the transversal direction periodic boundary conditions (Bloch conditions) are imposed. In particular, along the x-direction the flake is periodic with period ∆.
The origin along the y-axis is set on the first atom of the bottom layer (so the first atom of the top layer is at y=-acc*0.5 nm, where acc is the C-C distance, by default 0.144 nm).
The attributes of the classes are the following:
- Nc : (int) the number of atoms along the longitudinal direction.
- n : (int) the number of atoms along the transversal direction. It is equal to 2
- acc (double): Carbon to carbon distance expressed in nm.
- acc_tp (double): the distance between the top and the bottom layer.
- kmin (double): is the minimum value of the transversal wave vector in the Brillouin zone, over which the integral for the T and the charge is computed. By default it is set to 0.
- kmax (double): is the maximum value of the transversal wave vector in the Brillouin zone, over which the integral for the T and the charge is computed. By default it is set to pi/∆.
- dk (double): the wave vector step used for the computation of the charge and the T.
- Eupper : (double) the upper energy limit for which the NEGF is computed in the graphene bilayer.
- Elower : (double) the lower energy limit for which the NEGF is computed in the graphene bilayer.
- dE : (double) the energy step computed when solving the NEGF
- thop : (double) the hopping parameter of the pz tight-binding Hamiltonian between two in-plane carbon atoms.
- tp (double): the hopping parameter of the pz tight-binding Hamiltonian between two overlaying C atoms.
- eta : (double) the infinitesimal imaginary part used in the NEGF formalism
- mu1 : (double) the Fermi level of the left reservoir
- mu2 : (double) the Fermi level of the right reservoir
- Temp : (double) the temperature at which the charge and the current is computed
- E : (numpy array) array of the energies for which the transmission coefficient and the free charge is computed in the graphene bilayer by means of the NEGF formalism
- T : (numpy array) array of the transmission coefficient computed in correspondence of the energies stored in the E array
- charge : (numpy array of length n*Nc) free charge computed in correspondence of each C atom of the graphene bilayer. In the equilibrium case, mu1=mu2, the mobile charge on a given site on layer j (j = 1,2) of the bilayer graphene sheet reads
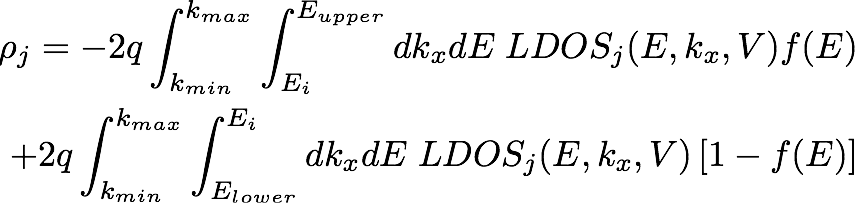 where q is the elementary charge, Ei is the intrinsic (midgap) Fermi level, f is the Fermi–Dirac occupation factor, LDOSj (E, kx, V ) is the local density of states on layer j, V is the potential difference between the top and the bottom layer, and the integral is performed along the k and E axis, with the limits sets above. Out of the equilibrium, both the Fermi Dirac with mu1 and mu2 have to be considered
where q is the elementary charge, Ei is the intrinsic (midgap) Fermi level, f is the Fermi–Dirac occupation factor, LDOSj (E, kx, V ) is the local density of states on layer j, V is the potential difference between the top and the bottom layer, and the integral is performed along the k and E axis, with the limits sets above. Out of the equilibrium, both the Fermi Dirac with mu1 and mu2 have to be considered - x : (numpy array of length n*Nc) the x position of the i-th atom of the graphene bilayer: it can be either 0 (if C atoms belongs to the bottom layer) or 0.35 nm (if the atom belongs to the top layer).
- y : (numpy array of length n*Nc) the y position of the i-th atom along the transport direction
- atoms_coordinates : (function) it computes the atoms coordinates in correspondence of each C atoms, filling the x, y vectors of the graphene bilayer class.
- L : (double) the effective length of the nanotube, which is the length of the graphene composed by a integer number of unit cells, closest to the length specified by the user.
- charge_T : (function) function which computes the transmission coefficient and the free charge in correspondence of each C atoms of the graphene bilayer flake. Such a computation is performed in the real space.
- current : (function) it computes the current through the Landuer formula, once filled the T vector.
- gap : (function) it computes the energy gap of the nanoribbon: it is set to tp.
- rank : (int) the rank of the process. This is required when using the MPIze_kt function
See the tutorial on bilayer graphene for a clear undestanding of this class.

